p-value check

Compare reported p-value with distribution of possible p-values.

library(tidyverse)
library(gt)
library(ggthemes)
library(glue)

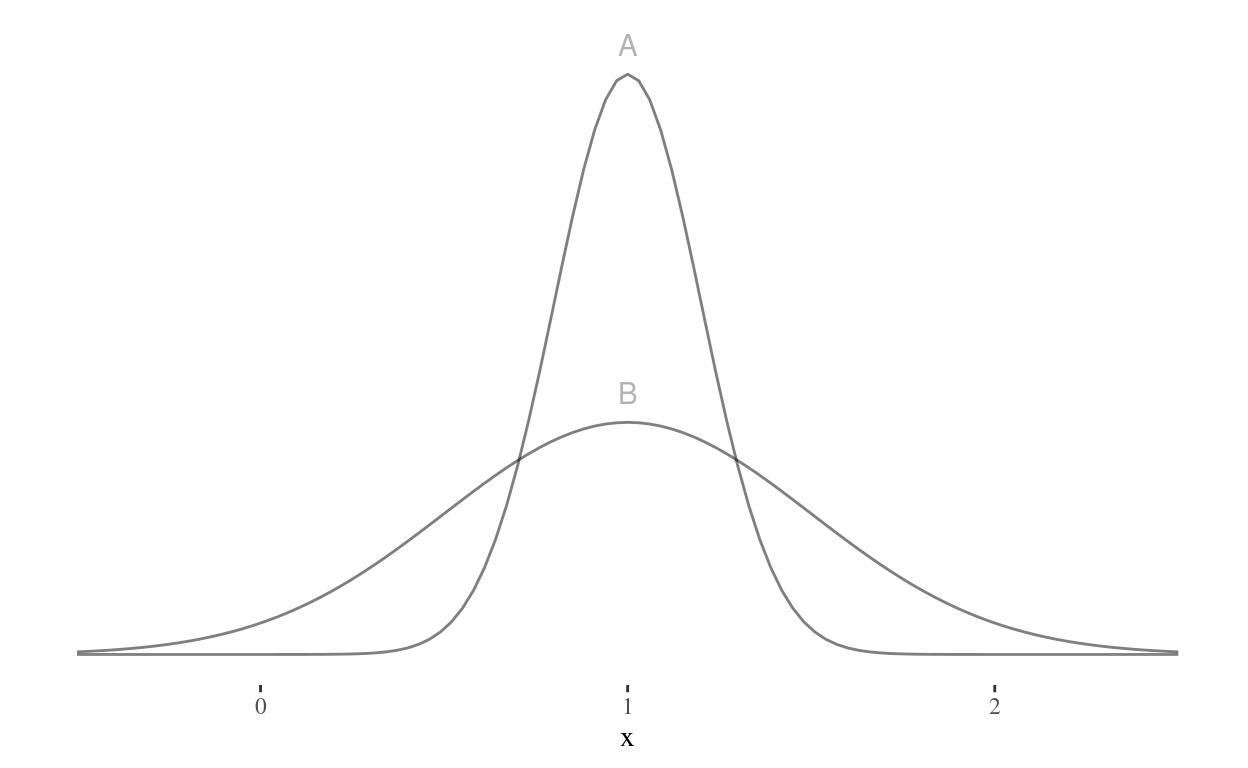
Suppose we have a study that has reported a p-value of for a t-test between groups A and B with the following means, standard deviations, and sample sizes.

dat <- 
  tibble(
    group = c("A", "B"),
    mean = c(params$amu, params$bmu),
    sd = c(params$asigma, params$bsigma),
    n = c(params$an, params$bn)
  )

dat %>% 
  gt()

group	mean	sd	n
A	1	0.2	35
B	1	0.5	50

dnorm(0.5, mean = c(0, 1), sd = c(1, 2))

[1] 0.3520653 0.1933341

pnorm(0.5, 0, 1)

[1] 0.6914625

ggplot() +
  stat_function(
    fun = dnorm,
    args = list(mean = params$amu, sd = params$asigma),
    alpha = 0.5
  ) +
  stat_function(
    fun = dnorm,
    args = list(mean = params$bmu, sd = params$bsigma),
    alpha = 0.5
  ) +
  geom_text(
    aes(x = x, y = y, label = label),
    data = tibble(
    x = c(params$amu, params$bmu),
    y = dnorm(c(params$amu, params$bmu), mean = c(params$amu, params$bmu), sd = c(params$asigma, params$bsigma)) + 0.1,
    label = c("A", "B")),
    alpha = 0.3) +
  theme_tufte() +
  theme(
    axis.line.y = element_blank(),
    axis.ticks.y = element_blank(),
    axis.text.y = element_blank(),
    axis.title.y = element_blank()
  ) +
  xlim(min(c(params$amu, params$bmu)) - 3 * max(c(params$asigma, params$bsigma)),
       max(c(params$amu, params$bmu)) + 3 * max(c(params$asigma, params$bsigma)))

Now we wish to write a simulation that draws a samples from each distribution of 35, 50, respectively, and computes a t-test, producing a p-value.

sample_a <- rnorm(params$an, mean = params$amu, sd = params$asigma)
sample_b <- rnorm(params$bn, mean = params$bmu, sd = params$bsigma)

sample_a %>% head()

[1] 1.0130998 1.0685929 0.6222748 0.9641765 1.0303178 1.1513003

sample_b %>% head()

[1]  0.6239472  0.6695744  0.5656617  1.0382910  0.1608477 -0.2904730

ttest <- t.test(sample_a, sample_b)

ttest

    Welch Two Sample t-test

data:  sample_a and sample_b
t = 1.0216, df = 63.378, p-value = 0.3109
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.08332685  0.25767415
sample estimates:
mean of x mean of y 
0.9886130 0.9014394 

# extract the p value
ttest$p.value

[1] 0.3108569

Now let’s turn this into a fucntion.

ptrial <- function(
  sim_id,
  amu = params$amu,
  bmu = params$bmu,
  asigma = params$asigma,
  bsigma = params$bsigma,
  an = params$an,
  bn = params$bn
){
  # get samples
  sample_a <- rnorm(n = an, mean = amu, sd = asigma)
  sample_b <- rnorm(n = bn, mean = bmu, sd = bsigma)
  
  # calculate t-test
  ttest <- t.test(sample_a, sample_b)
  
  # return pvalue
  return(
    tibble(
      id = sim_id,
      p_value = ttest$p.value
    )
  )
}

ptrial(1)

# A tibble: 1 × 2
     id p_value
  <dbl>   <dbl>
1     1   0.374

Now that we have a function, we can perform 120 trials.

trials <- 
1:params$trials %>% 
  map_df(ptrial)

trials %>% head() %>%  gt()

id	p_value
1	0.03004456
2	0.99581508
3	0.06373585
4	0.36094549
5	0.98282944
6	0.88825267

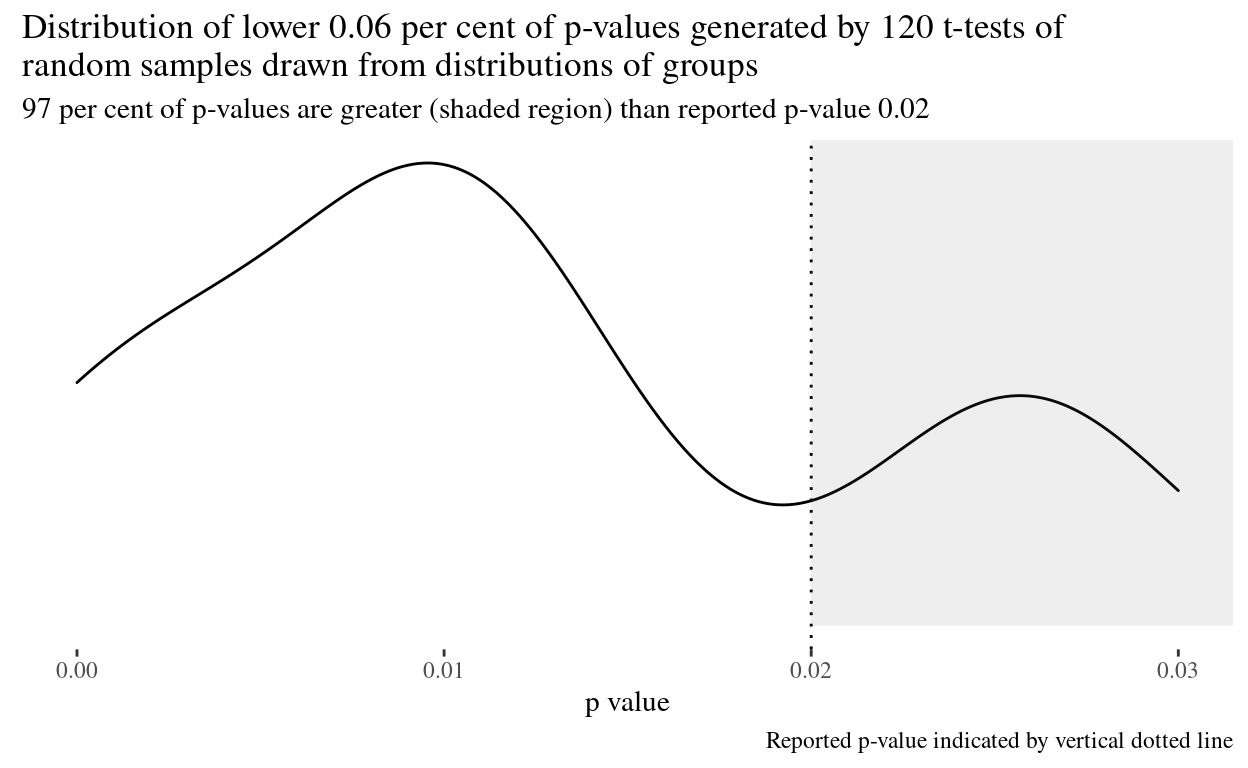
Now we plot the distribution of p-values.

reported_quant <- ecdf(trials$p_value)(params$reportedp)

shown_p <- params$reportedp + params$reportedp/2

shown_percent <- ecdf(trials$p_value)(shown_p) %>% round(2) * 2

trials %>% 
  ggplot(aes(x = p_value)) +
  geom_density() +
  theme_tufte() +
    theme(
    axis.line.y = element_blank(),
    axis.ticks.y = element_blank(),
    axis.text.y = element_blank(),
    axis.title.y = element_blank()
  ) +
  geom_vline(
    xintercept = params$reportedp,
    linetype = "dotted"
  ) +
  annotate(
      "rect",
      xmin = params$reportedp,
      xmax = Inf,
      ymin = 0,
      ymax = Inf,
    alpha = 0.1
    ) +
  labs(
    title = str_wrap(glue("Distribution of lower {shown_percent} per cent of p-values generated by {params$trials} t-tests of random samples drawn from distributions of groups")),
    subtitle = str_wrap(glue("{(1 - round(reported_quant, 2)) * 100} per cent of p-values are greater (shaded region) than reported p-value {params$reportedp}")),
    x = "p value",
    caption = "Reported p-value indicated by vertical dotted line"
  ) +
  xlim(0, shown_p)